voxelmorph学习笔记

VoxelMorph: A Learning Framework for Deformable Medical Image Registration

令$f$ 表示 fixed image，$m$表示 moving image，$\phi$ 为 registration field.

$$\begin{align*} \widehat {\phi }=&\mathop {\mathrm {arg\,min}} _{\phi }\mathcal {L}(f, m, {\phi }) \tag{1}\\=&\mathop {\mathrm {arg\,min}} _{\phi } \mathcal {L}_{sim}(f, m\circ {\phi }) + \lambda \mathcal {L}_{smooth}({\phi }),\tag{2}\end{align*}$$

通常，$\phi$ 可以是 displacement vector field $\mathbf{u}$，指定了 $f$ 到 $m$ 的 vector offset：${\phi }= Id + \mathbf{u}$.

传统算法针对每个 volume pair 优化公式（1）。 相反，我们假设可以通过数据的参数化函数来计算 a field。 我们通过最小化体积对数据集上的（1）形式的期望能量来优化函数参数。 从本质上讲，我们用共享参数的全局优化来代替变形场的特定于对的优化，在其他领域，这被称为amortization。 一旦估计了全局函数，就可以通过在给定的体积对上评估函数来产生一个场。 在本文中，我们使用 displacement-based vector field representation，并着重于学习框架的各个方面及其优势。 但是，我们最近证明了在类似于VoxelMorph的框架中也可以进行 velocity-based representations.

使用 CNN 建模一个函数 $g_{\theta }(f, m) = \mathbf {u}$，其中，$\theta$ 是 CNN 的参数，displacement field $\mathbf{u}$ 存储于一个 ${n+1}$-维 的图像中。也就是说，对于每个像素 $\mathbf {p} \in \Omega$，$\mathbf {u}~(\mathbf {p})$ 是一个 displacement，that $f(\mathbf{p})$ 和 $[m\circ{\phi}] \mathbf{(p)}$ 对应于相似解剖位置，其中，${\phi }= Id + \mathbf{u}$ 由 一个 identity transform 和 $\mathbf{u}$ 构成。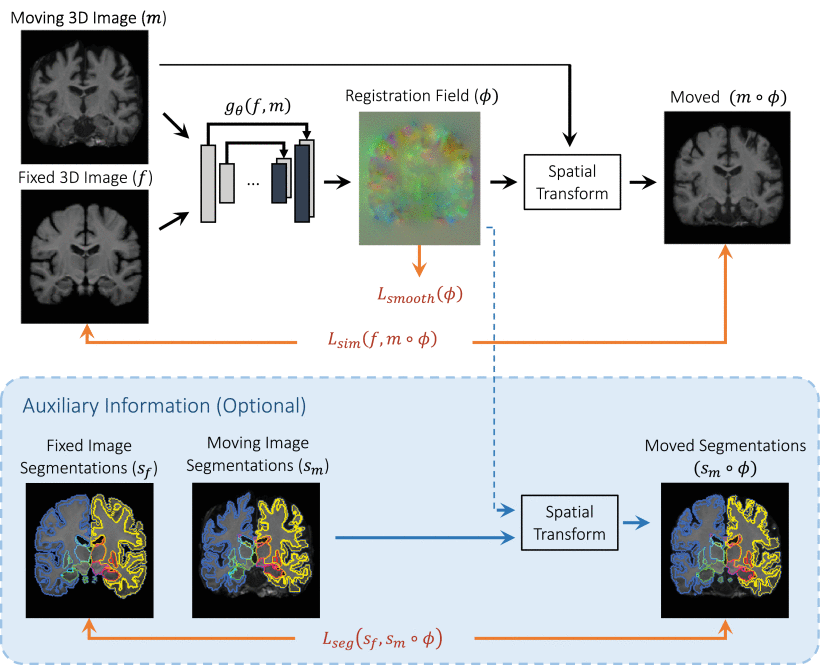

作者提出了两个无监督的损失函数。 第一个捕获 image similarity 和 field smoothness，而第二个也利用解剖学分割。

A. VoxelMorph CNN Architecture

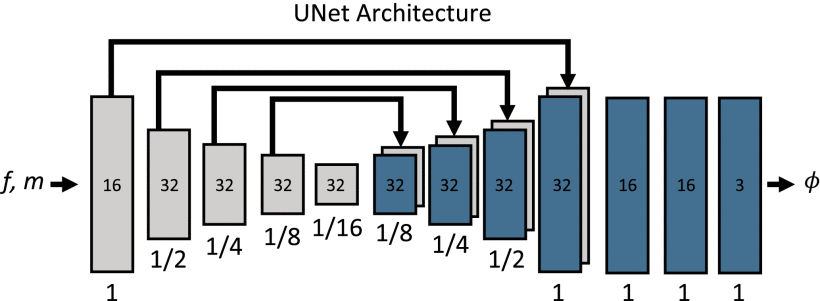
简单的U-Net结构，输入为 2 channel 的 $f$ 和 $m$ 的级联。

B. Spatial Transformation Function

本文方法通过最小化 $m\circ{\phi}$ 和 $f$ 之间的差异来部分学习最佳参数值。 为了使用基于梯度的标准方法，本文基于 spatial transformer networks 构造了可微分运算来计算 $m\circ{\phi}$.

对于每个voxel $\mathbf{p}$，我们计算 $m$ 中的一个 voxel 位置 $\mathbf{p}^{\prime }=\mathbf{p}+ \mathbf{u}(\mathbf{p})$. 因为图像值仅在整数位置定义，所以我们在八近邻体素处线性插值：

$$\begin{equation*} m\circ {\phi }(\mathbf {p}) = \sum _{\mathbf {q} \in \mathcal {Z}(\mathbf {p}^{\prime })} m(\mathbf {q}) \prod _{d \in \{x,y,z\}} (1-| \mathbf {p}^{\prime }_{d} - \mathbf {q}_{d}|),\tag{3}\end{equation*}$$

C. Loss Functions

作者提出两个损失函数：一个无监督的损失 $\mathcal{L}_{us}$，它仅使用 input volumes 和 generated registration field 来评估模型，以及一个辅助损失 $\mathcal{L}_{a}$，它在训练时利用了解剖学上的分割。

1) Unsupervised Loss Function:

无监督损失 $\mathcal{L}_{us}(\cdot,\cdot,\cdot)$ 包括 2 个成分：

• $\mathcal{L}_{sim}$：惩罚外观差异
• $\mathcal{L}_{smooth}$：惩罚 $\phi$ 中的局部空间变化：

$$\begin{equation*} \mathcal {L}_{us}(f, m, {\phi }) = \mathcal {L}_{sim}(f, m\circ {\phi }) + \lambda \mathcal {L}_{smooth}({\phi }), \tag{4}\end{equation*}$$

作者为 $\mathcal{L}_{sim}$ 实验了两个常用函数。 第一个是体素均方差，适用于 $f$ 和 $m$ 具有相似的图像 intensity distributions 和 local contrast 的情况：

$$\begin{equation*} MSE(f, m\circ {\phi }) = \frac {1}{|\Omega |}\sum _{p \in \Omega } \left [{ f(\mathbf {p}) - [m\circ {\phi }] (\mathbf {p}) }\right]^{2}.\tag{5}\end{equation*}$$

第二个是 $f$ 和 $m\circ{\phi }$ 的 local cross-correlation，它对不同数据之间的强度变化更健壮。 令 $\hat{f}({\mathbf{p}})$ 和
$[\hat{m}\circ{\phi}]\mathbf{(p)}$ 表示具有 local mean intensities 的图像：$\hat{f}({\mathbf{p}})=\frac{1}{n^{3}}\sum _{\mathbf{p}_{i}}f\,\,(\mathbf{p}_{i})$，其中 $\mathbf{p}_{i}$ 遍历 $\mathbf{p}$ 周围的 $n^{3}$ volume，其中 $n=9$。 $f$ 和 $m\circ{\phi }$ 的 local cross-correlation 写为：

$$\begin{align*}&\hspace{-1.5pc}CC(f, m\circ {\phi }) \\&\hspace{-1.3pc}=\!\sum \limits _{ \mathbf {p}\in \Omega }\!\frac {\left ({\!\sum \limits _{ \mathbf {p}_{i}} (f({ \mathbf {p}_{i}})\!-\!\hat { f} ({ \mathbf {p}}))([m\circ {\phi }] ({ \mathbf {p}_{i}})\!-\![\hat { m} \circ {\phi }] ({ \mathbf {p}}))\!}\right)^{2}}{\left ({\!\sum \limits _{ \mathbf {p}_{i}} (f({ \mathbf {p}_{i}})\!-\!\hat { f} ({ \mathbf {p}}))^{2}\!}\right)\left ({\sum \limits _{ \mathbf {p}_{i}} ([m\circ {\phi }] ({ \mathbf {p}_{i}})\!-\![\hat { m}\circ {\phi }] ({ \mathbf {p}}))^{2}\!}\right)}.\!\!\!\!\!\!\! \\\tag{6}\end{align*}$$

CC越高表示对齐越好，产生损失函数：$\mathcal{L}_{sim}(f, m, {\phi}) = -CC(f,m\circ{\phi})$.

使 $\mathcal{L}_{sim}$ 最小化将鼓励 $m\circ{\phi}$ 近似于 $f$，但可能会生成在物理上不现实的非平滑 ${\phi}$。 我们鼓励在 displacement $\mathbf{u}$ 的空间梯度上使用 diffusion regularizer 来获得平滑的 displacement field ${\phi}$:

$$\begin{equation*} \mathcal {L}_{smooth}({\phi }) = \sum _{ \mathbf {p}\in \Omega } \lVert \nabla { \mathbf {u}(\mathbf {p})} \rVert ^{2},\tag{7}\end{equation*}$$

并使用相邻体素之间的差异来估算空间梯度。具体来说，对于 $\nabla \mathbf {u} (\mathbf {p}) = \left ({\frac {\partial \mathbf {u} (\mathbf {p})}{\partial x}, \frac {\partial \mathbf {u}(\mathbf {p})}{\partial y}, \frac {\partial \mathbf {u} (\mathbf {p})}{\partial z}}\right)$ , 近似 $\frac {\partial \mathbf {u}(\mathbf {p})}{\partial x} \approx \mathbf {u} ((p_{x} + 1, p_{y}, p_{z})) - \mathbf {u}((p_{x}, p_{y}, p_{z}))$ , 并对 $\frac {\partial \mathbf {u} (\mathbf {p})}{\partial y}$ 和 $\frac {\partial \mathbf {u}(\mathbf {p})}{\partial z}$ 使用similar approximations.

2) Auxiliary Data Loss Function:

在这里，我们描述了 VoxelMorph 如何利用训练期间而不是测试期间可用的辅助信息。 解剖分割图有时在训练过程中可用，并且可以由人类专家或自动算法进行注释。 分割图将每个体素分配给一个解剖结构。 如果配准场 $\phi$ 表示精确的解剖学对应关系，则 $f$和 $m\circ{\phi}$ 中与同一解剖结构相对应的区域应很好地重叠。

$$\begin{equation*} \text {Dice}(s_{f}^{k}, s^{k}_{m} \circ {\phi }) = 2 \cdot \frac {| s^{k}_{f} \cap (s^{k}_{m} \circ {\phi })|}{| s^{k}_{f}| + | s^{k}_{m} \circ {\phi } |}. \tag{8}\end{equation*}$$ $$\begin{equation*} \mathcal {L}_{seg}(s_{f}, s_{m} \circ {\phi }) = - \frac {1}{K} \sum _{k=1}^{K} \text {Dice}(s^{k}_{f}, s^{k}_{m} \circ {\phi }). \tag{9}\end{equation*}$$

单独使用 $\mathcal {L}_{seg}$ 并不能提高图像外观的平滑度和一致性，而这对于良好的配准至关重要。 因此，我们将 $\mathcal {L}_{seg}$ 与（4）结合起来以达到目标：

$$\begin{align*}&\hspace{-1.6pc}\mathcal {L}_{a}(f, m, s_{f}, s_{m}, {\phi }) \\&\qquad \qquad \quad =\mathcal {L}_{us}(f, m, {\phi }) + \gamma \mathcal {L}_{seg}(s_{f}, s_{m} \circ {\phi }), \tag{10}\end{align*}$$

D. Amortized Optimization Interpretation

Experiments

使用了 3731 T1–weighted brain MRI scans from eight publicly available datasets: OASIS, ABIDE, ADHD200, MCIC, PPMI, HABS, Harvard GSP, 和 FreeSurfer Buckner40. All scans were resampled to a $256\times 256 \times 256$ grid with 1mm isotropic voxels. 使用了标准的预处理步骤，包括 affine spatial normalization and brain extraction for each scan using FreeSurfer，并将图像 crop 到 $160\times 192 \times 224$. 所有的 MRI 图像均使用 FreeSurfer 自动分割，并进行了质量控制。

使用 Symmetric Normalization (SyN) 作为第一个 baseline. 在开源的高级归一化工具（ANTs）软件包中实现SyN，with a cross-correlation similarity measure. 在处理医学图像的整个过程中，我们发现默认的ANTs平滑度参数对于将ANTs应用于我们的数据而言不是最理想的。 我们使用跨多个数据集的广泛参数扫描获得了改进的参数，并在这些实验中使用了这些参数。 具体来说，我们使用0.25的SyN步长，高斯参数（9，0.2），三个尺度，每个尺度最多201次迭代。 我们还将NiftyReg软件包用作第二个基准。 不幸的是，目前还没有GPU实现，而是我们构建了多线程CPU版本。我们搜索了各种参数设置以获得改进的参数，并使用CC cost function, grid spacing of 5, and 500 iterations.

Our code and model parameters are available online at https://github.com/voxelmorph/voxelmorph.